Symmetrically Speaking

Writing and Playing with Particular Non-Diatonic Sonorities

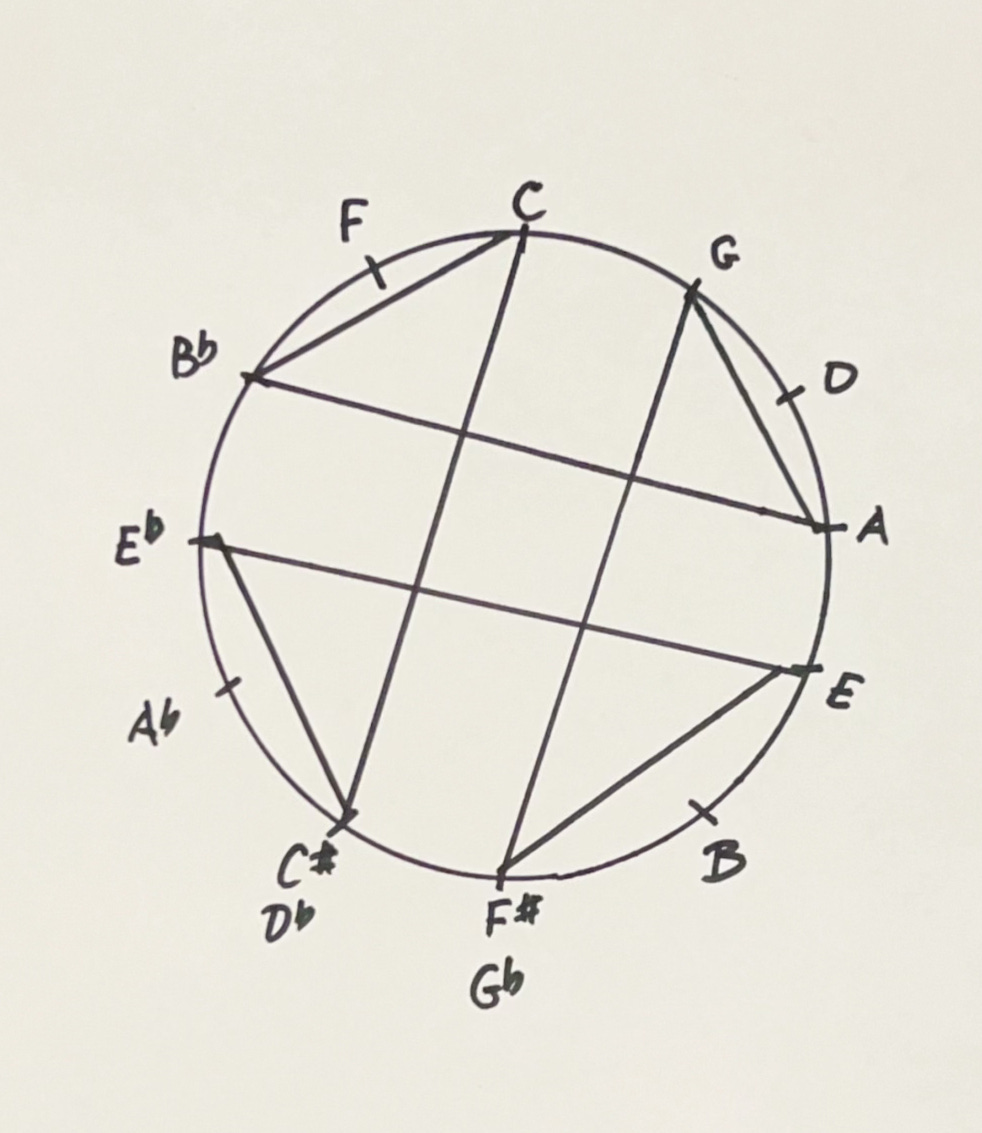
Above is a visual representation of the symmetricality of the half-step/whole-step symmetrical diminished scale.

Improvisors will often superimpose notes and phrases derived from the symmetrical diminished scale in its repeating half-step/whole-step pattern when the composition shows a dominant seventh chord.

On a C7 chord, that same intervallic pattern, half/whole, being an octatonic scale, makes available both b9 and #9. #11 and natural 13 as well as a natural 5. With symmetrical scales all the intervallic shapes repeat every minor third, but from the new pitch.

What we are considering now, rather than a formidable tactic to place altered upper voices on a chord in a diatonic context, is looking at symmetrical shapes and patterns as a way for composers to create sonic environments for improvisers and listeners alike.

For each half/whole sym dim scale there are four equidistant roots, each a minor third apart. Chords and melody derived from this scale can evoke ambiguity while any internal dissonances can be balanced by nimble resolution.

The vast harmonic world within h/w sym dim is evident when looking at all the chords it produces. If we start with a C tonic, which is simultaneously an A, F# and Eb tonic) we have these triads from each of the co-equal root. In other words, there are four of each of these chords.

Chords Built On The Four Equidistant Tonics of the Half-Step/Whole-Step Symmetrical Diminished Scale - starting on C, for example

Triads

Root 3 5 - major triad, C, A, F# Eb

R b3 5 - minor, Cm, Am, F#m, Ebm or its enharmonic equivalent, R #2 5 - (sus#2), C(sus#2), etc.

R b2 5 - C(sus b2), A(sus b2), F#(sus b2), Eb(sus b2)

R #4 5 - C(sus#4), A(sus#4), F#(sus#4), Eb(sus#4)

R 3 b5 - C(b5), A(b5), F#(b5), Eb(b5)

R b3 b5 - Co, Ao, F#o, Ebo

R b2 b5 - C(b5)sus b2, A(b5)sus b2, F#(b5)sus b2, Eb(b5)sus b2                                                     or enharm. R b2 #4 - C(sus b2,#4), etc.

Added-note chords and their inversions as slash chords with added note in bass

R b2 3 5 - C(add b2), A(add b2), F#(add b2), Eb(add b2), C/Db, A/Bb, F#/G, Eb/E

R #2 3 5 - C(add#2), A(add#2), F#(add#2), Eb(add#2), C/Eb, A/C, F#/A, Eb/Gb

R #4 3 5 - C(add#4), A(add#4), F#(add#4), Eb(add#4), C/F#, A/Eb, F#/C, Eb/A

R b2 b3 5 - Cm(add b2), Am(add b2), F#m(add b2), Ebm(add b2), Cm/Db, Am/Bb, F#m/G, Ebm/E

R #4 b3 5 - Cm(add#4), Am(add#4), F#m(add#4), Ebm(add#4), Cm/F#, Am/Eb, F#m/C, Ebm/A

R b2 b3 b5 - Co(add b2), Ao(add b2), F#o(add b2), Ebo(add b2), Co/Db, Ao/Bb, F#o/G, Ebo/E

Seventh Chords

R 3 5 b7 - C7, A7, F#7, Eb7

Upper Voices

b9 #9 #11 13 (singly or in any combination)

This of course only using half the scale. The remaining notes, again equidistant by a minor third, exist a half-step above each of our root notes. In this case they’d be Db, E, G and Bb.

Chords Built On The Four Remaining Tones of the Half-Step/Whole-Step Symmetrical Diminished Scale

Triads

R b3 b5 - Dbo, Eo, Go, Bbo

R 2 b5 - Dbo(sus2), Eo(sus2), Go(sus2), Bbo(sus2)

R 4 b5 - Dbo(sus4), Eo(sus4), Go(sus4), Bbo(sus4)

Added-note Chords and their inversions as slash chords with added note in bass

R 2 b3 b5 - Dbo(add2), Eo(add2), Go(add2), Bbo(add2), Dbo/Eb, Eo/F#, Go/A, Bbo/C

R 4 b3 b5 - Dbo(add4), Eo(add4), Go(sus4), Bbo(add4), Dbo/Gb, Eo/A, Go/C, Bbo/Eb

Seventh Chords

R b3 b5 bb7 - Dbo7, Eo7, Go7, Bbo7

R b3 b5 7 - Dbo(maj7), Eo(maj7), Go(maj7), Bbo(maj7)

Upper Voices

9 11 b13 (singly or in any combination)

So here is an entire cosmos of harmony contained within eight tones symmetrically extracted from the twelve equally tempered tones of what originated as Western music as it applies to classical music, jazz and pop music. This is what music theorist Dmitri Tymoczko calls The Extended Common Practice.

Above is an example of sonorities derived from a C (or A or F# or Eb) H/W sim dim resolving to a lydian chord.

I continue to plan on publishing all of my compositions here as well as much more content when, sometime in the near future, I institute paid subscriptions.

Meanwhile, please subscribe.

Material will continue to be available for free subscribers, similar in scope to what has already been coming out.

Copyright © 2024 Jack DeSalvo